Inhalt der Vorlesung
Einführung in die numerischen Methoden zur Behandlung mechanischer Systeme. Grundlagen der numerischen Mathematik: Numerische Prinzipe, Maschinenzahlen, Fehleranalyse. Lineare Gleichungssysteme: Cholesky-Zerlegung, Gauß-Elimination, LR-Zerlegung, QR-Zerlegung, iterative Methoden bei quadratischer Koeffizientenmatrix, Lineares Ausgleichsproblem. Eigenwertproblem: Grundlagen, Normalformen, Vektoriteration, Berechnung von Eigenwerten mit dem QR-Verfahren, Berechnung von Eigenvektoren. Anfangswertproblem bei gewöhnlichen Differentialgleichungen: Grundlagen, Einschrittverfahren (Runge-Kutta Verfahren), Extrapolationsverfahren, Mehrschrittverfahren. Werkzeuge und numerische Bibliotheken für lineare Gleichungssysteme, Eigenwertprobleme und Anfangswertprobleme. Theorie und Numerik in der Anwendung - ein Vergleich.
Informationen zur Vorlesung
Vorlesung und Vortragsübungen
- Für Studierende der Studiengänge Maschinenwesen, Mechatronik, Techischer Kybernetik, Technologiemanagement, Fahrzeug- und Motorentechnik, Mathematik und Commas.
- Die Vorlesung findet vollständig in Präsenz statt.
- Montags, 11.30 - 13.00 Uhr im Hörsaal V55.01
Donnerstags, 11.30 - 13.00 Uhr im Hörsaal V47.04 - Die erste Vorlesung im Sommersemester 2025 findet am Montag, den 7. April 2025 statt.
Vorlesungsunterlagen
Aufgaben- und Merkblätter finden Sie bei den Unterlagen.
Sprache
Die Vorlesung wird in deutscher Sprache gehalten.
Institut
Die Räume des Institut für Technische und Numerische Mechanik befinden sich im Ingenieurwissenschaftlichen Zentrum (IWZ), Pfaffenwalding 9, 3. und 4. Stock.
Kontakt
- 1. Einleitung
- 2. Grundlagen der Numerischen Mathematik
- 2.1 Begriffe
- 2.2 Numerische Prinzipe
- 2.3 Maschinenzahlen
- 2.4 Fehleranalyse
- 3. Lineare Gleichungssysteme
- 3.1 Problemstellung
- 3.2 Direkte Methoden bei quadratischer Koeffizientenmatrix
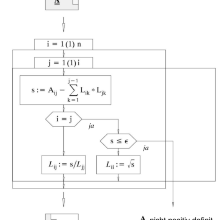
- 3.3 Cholesky-Zerlegung
- 3.4 Gauss-Elimination
- 3.5 LR-Zerlegung
- 3.6 QR-Zerlegung
- 3.7 Iterative Methoden bei quadratischer Koeffizientenmatrix
- 3.8 Determinante einer Matrix
- 3.9 Inverse einer Matrix
- 3.10 Lineares Ausgleichsproblem
- 3.11 Werkzeuge und numerische Bibliotheken für lineare Gleichungen
- 4. Eigenwertproblem
- 4.1 Grundlagen
- 4.2 Normalformen
- 4.3 Vektoriteration
- 4.4 Berechnung von Eigenwerten mit dem QR-Verfahren
- 4.5 Berechnung von Eigenvektoren
- 4.6 Praktische Lösung des Eigenwertproblems
- 4.7 Werkzeuge und numerische Bibliotheken für Eigenwertprobleme
- 5. Anfangswertprobleme bei gewöhnlichen Differentialgleichungen
- 5.1 Problemstellung
- 5.2 Grundlagen
- 5.3 Einschrittverfahren
- 5.4 Extrapolationsverfahren
- 5.5 Mehrschrittverfahren
- 5.6 Vergleich der Verfahren
- 5.7 Werkzeuge und numerische Bibliotheken für Anfangswertprobleme
Aktuelles
Vorlesungsbeginn
Die Vorlesung beginnt am 7. April um 11:30 Uhr.
Pascal Ziegler
Dr.-Ing., Akademischer Oberrat