Bild: (c) Technische Universität München
Bild: (c) www.nasa.gov
Bild: (c) www.nasa.gov
Motivation
- Mechanische Strukturen mit geometrischen Nicht-linearitäten werden in vielen Anwendungen eingesetzt
- Immer größer werdende mathematische Modelle
→ Simulation und Analyse sehr rechenintensiv - Ziel: Modellordnungsreduktion (MOR) für nichtlineare, parametrische Systeme 2. Ordnung
zur effizienten Simulation, Analyse und Auslegung von “calm, smooth and smart” Strukturen
Wahl der reduzierten Basis
- Projektive MOR: Approximation der Freiheitsgrade durch reduzierte Koordinaten mit Hilfe der Basis V
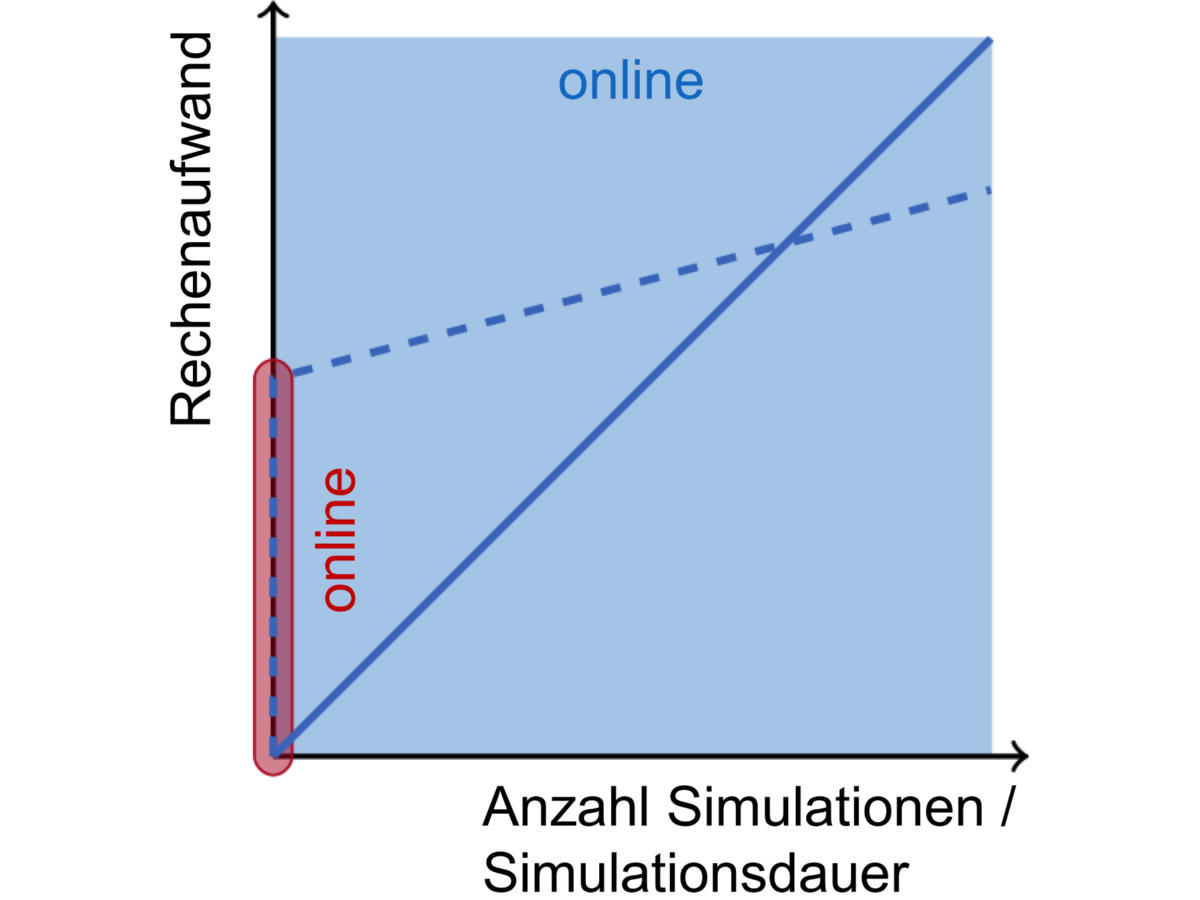
- Stand der Technik: Simulationsbasierte Methoden (POD-Verfahren), die auf teuren Simulationen des Originalmodells beruhen
- Kernidee: Simulationsfreie Berechnung der Basis V
Methoden
- Modale Ableitungen → Methode basierend auf die Erweiterung der linearen Basis V mit modalen Ableitungen
- Kombination von modalen Ableitungen mit Krylow-Unterraummethoden
- Berechnung einer parametrischen Basis V(p) mit Hilfe von Verfahren der parametrischen Modellreduktion (pMOR)
Hyper-Reduktion
- Berechnung der nichtlinearen Terme wird bei projektiver MOR nicht beschleunigt (nur Lösung des Gleichungssystems wird beschleunigt)
- Assemblierung des nichtlinearen Kraftvektors ist neuer Flaschenhals
- Kernidee: Reduktion des Netzes, so dass nur wenige finite Elemente ausgewertet werden müssen
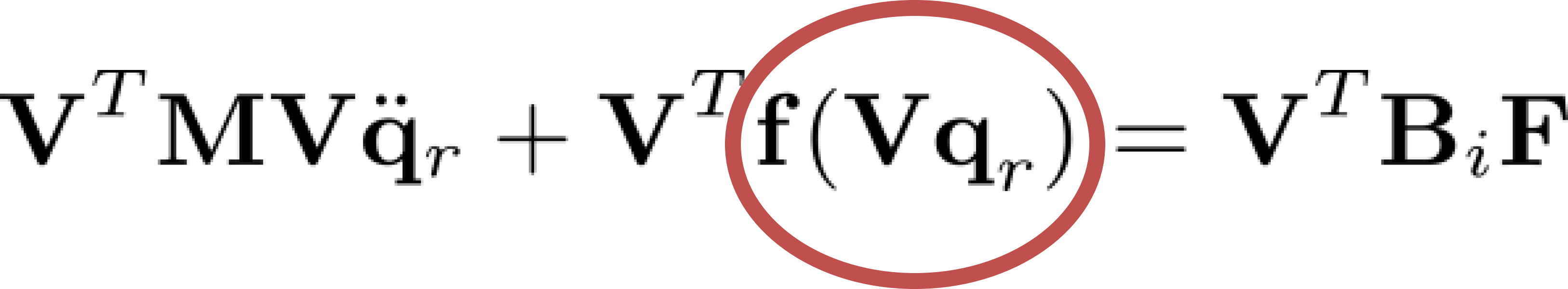
Methoden
- ECSW: Energy Conserving Mesh Sampling and Weighting
→ Methode basierend auf Prinzip der virtuellen Arbeit - DEIM: Discrete Empirical Interpolation Method
→ Approximation des unreduzierten Modells
Wissenschaftliche Ziele/Arbeitsprogramm
- Berechnung der reduzierten Basis
- mit simulationsfreien Verfahren (z.B. mit modalen Ableitungen und Krylow)
- Berechnung der Basen für verschiedene Parametersätze
- durch Nutzung von pMOR-Verfahren
- Entwicklung von simulationsfreien Hyperreduktionsmethoden
- basierend auf DEIM, ECSW
- Entwicklung von simulationsfreien Hyperreduktionsmethoden für parametrische nichtlineare Systeme
- Validierung anhand von Benchmarkmodelle und Fallstudien
Kontakt
Prof. Dr.-Ing. habil. Boris Lohmann
Lehrstuhl für Regelungstechnik
Technische Universität München
Boltzmannstraße 15
85748 Garching
Tel.: +49 089 289-15610
E-Mail: lohmann@tum.de
Prof. Dr. Daniel J. Rixen, M.Sc.
Lehrstuhl für Angewandte Mechanik
Technische Universität München
Boltzmannstraße 15
85748 Garching
Tel.: +49 089 289-15220
E-Mail: rixen@tum.de
Christopher Lerch, M.Sc. (hons)
Tel.: +49 089 289-15677
E-Mail: christopher.lerch@tum.de
Christian Meyer, M.Sc.
Tel.: +49 (89) 289 - 15202
E-Mail: christian.meyer@tum.de
Maria Cruz Varona, M.Sc.
Tel.: +49 (89) 289 - 15592
E-Mail: maria.cruz@tum.de
Dipl.-Ing. (Univ.) Johannes Rutzmoser
Tel.: +49 (89) 289 - 15202
E-Mail: johannes.rutzmoser@tum.de