Content of the lecture
Introduction to numerical methods used for investigating dynamic systems. General principles of numerical calculations, machine numbers, error estimation, numerical stability, linear algebra: Cholesky-decomposition, Gaussian elimination, LU-decomposition, QR-decomposition, iterative methods, least square problem, eigenvalue problem: general basics, normal forms, power methods, QR-algorithm, computaion of eigenvectors, initial value problem: ordinary differential equations, Runge-Kutta methods with step size control, extrapolation methods, linear multistep methods, -applications, programme libraries, comparison of methods for analytical investigations with computational methods.
Course information
Lecture and Exercises
For students of Mechanical engineering, Mechatronics, Mathematics and the interdisciplinary Graduate Study Programme COMMAS.
Monday, 11.30 a.m. - 1.00 p.m., V55.01.
Thursday, 11.30 a.m. - 1.00 p.m., V47.04.
First lecture in the summer term 2025 is on Monday, 7. April 2025.
Course Materials
Handouts to the lecture and the exercises are available for download
Language
The course is tought in German.
Institute
The Institute of Engineering and Computational Mechanics is located in Pfaffenwaldring 9, 3rd and 4th floor.
Contact
- 1. Introduction
- 2. General principles of numerical calculations
- 2.1 Definitions
- 2.2 Numerical principals
- 2.3 Machine numbers
- 2.4 Error estimation
- 3. Systems of linear algebraic equations
- 3.1 Motivation
- 3.2 Direct methods for square coefficient matrix
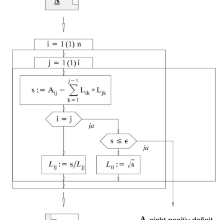
- 3.3 Cholesky-decomposition
- 3.4 Gauss-elimination
- 3.5 LR-decomposition
- 3.6 QR-decomposition
- 3.7 Iterative methodes for square coefficient matrix
- 3.8 Determinant of a matrix
- 3.9 Matrix inversion
- 3.10 Least square problem
- 3.11 Tools and numerical libraries for linear algebraic equations
- 4. Eigenvalue problems
- 4.1 General basics
- 4.2 Normal forms
- 4.3 Power methods
- 4.4 QR-algorithm
- 4.5 Calculation of eigenvectors
- 4.6 Practical solution of eigenvalue problems
- 4.7 Tools and numerical libraries for eigenvalue problems
- 5. Initial value problem for ordinary differantial equations
- 5.1 Motivation
- 5.2 Basic remarks
- 5.3 Single-step methods
- 5.4 Extrapolation methods
- 5.5 Multistep methods
- 5.6 Comparison of the different methods
- 5.7 Tools and numerical libraries for initial value problems
The lecture is supplemented by exercises. The exercises are discussed in class by Dr.-Ing. Pascal Ziegler. The documents are avaliable on the german webpage of the course.
Current information
Current information can be found on the German Webpage.

Pascal Ziegler
Dr.-Ing., Akademischer Oberrat