Motivation
Mechanische Systeme
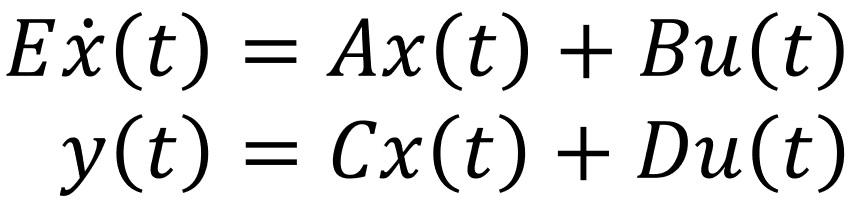
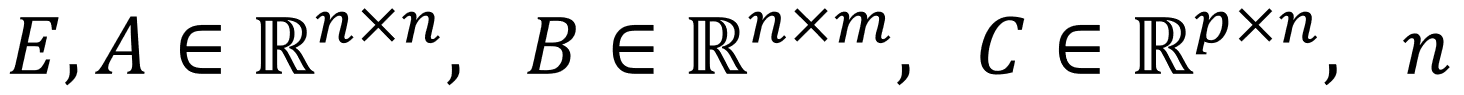
"sehr groß"
"Dissipativität ≙ Energie wird nur abgegeben"
Foto: Fraunhofer IWU Chemnitz/Dresden
Adaptive Spindelhalterung: CAD-Modell (links) and reale auf Prüfstand 3 POD montierte Komponente (rechts)
Foto: Max-Planck-Institut für Dynamik komplexer technischer Systeme, Universität Hamburg, Technische Universität Berlin
Wissenschaftliche Ziele
Modellreduktion mechanischer Systeme unter Erhaltung der Systemstruktur
darunter
- “zweite-Ordnung-Struktur”
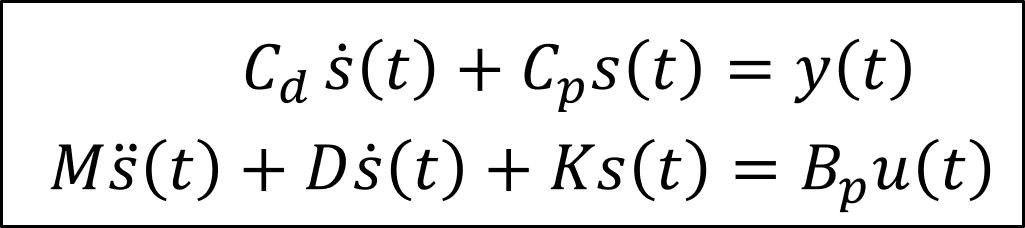
- Tor-Hamiltonische Systeme
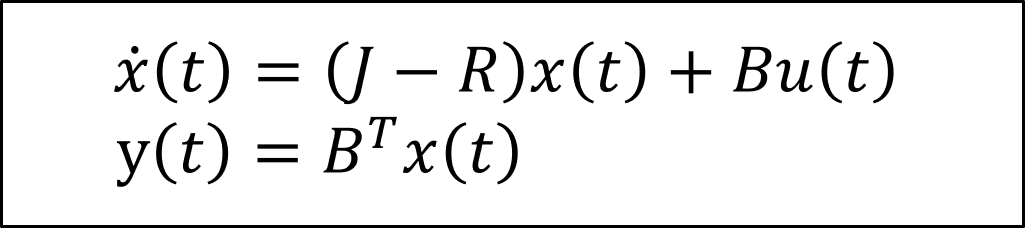
- Dissipativität
- Struktur von mechanischen Systemen
Quelle: de.wikipedia.org
Arbeitsprogramm
- Dissipativitätserhaltende Modellreduktion mechanischer Systeme
- Kombination von gängigen Verfahren mit anschließender “Störung”, so dass gegebene Struktur wiederhergestellt wird
- Ausnutzung der Systemstruktur zur Beschleunigung der numerischen Modellreduktionsverfahren
- Miteinbeziehung von (nicht-)holonomen Nebenbedingungen
Foto: Max-Planck-Institut für Dynamik komplexer technischer Systeme, Universität Hamburg, Technische Universität Berlin
Kontakt
Prof. Dr. Peter Benner
Max-Planck-Institut für Dynamik komplexer technischer Systeme
Sandtorstraße 1
39106 Magdeburg
benner@mpi-magdeburg.mpg.de
Prof. Dr. Timo Reis
Universität Hamburg
Bundesstraße 55
20146 Hamburg
timo.reis@uni-hamburg.de
Dr. Matthias Voigt
Technische Universität Berlin
Straße des 17. Juni 136
10246 Berlin
mvoigt@math.tu-berlin.de
Steffen Werner
Max-Planck-Institut für Dynamik komplexer technischer Systeme
Sandtorstraße 1
39106 Magdeburg
Ines Dorschky
Universität Hamburg
Bundesstraße 55
20146 Hamburg